Số phức nghịch đảo là nội dung rất quan trọng trong đại số lớp 12. Các bài tập về số phức nghịch đảo thường xuất hiện trong nhiều đề thi quan trọng. Tuy nhiên, không phải học sinh nào cũng nắm được rõ số phức nghịch đảo là gì? Và cách giải thế nào cho chính xác. Từ đó dẫn tới quá trình sai sót trong khi làm bài tập. Cùng Trungkhithe tìm hiểu chi tiết về Số phức nghịch đảo trong bài viết dưới đây.
Contents
Số phức nghịch đảo là gì?
Trước khi nói về số phức nghịch đảo thì ta cần tìm hiểu qua về số phức. Trong đó, số phức (Complex number) là số được viết dưới dạng α + bi (i² = -1) trong đó thì α, b là phần số thực còn i là phần số ảo. Số phức thuộc tập số thực có ký hiệu là z với z = a + bi.

Do đó số phức nghịch đảo của số phức là số phức có dạng sao cho tích của số phức nghịch đảo với số phức z bằng 1 có ký hiệu là z-1.
Chứng minh số phức nghịch đảo
Ta có thể chứng minh của số phức như sau:

Các bài tập về số phức nghịch đảo
Bài tập về số phức nghịch đảo có rất nhiều trong các đề thi, từ tốt nghiệp cho đến thi đại học. Do đó để đạt được điểm cao thì không thể bỏ qua các bài tập về số phức nghịch đảo. Dưới đây là một số dạng bài số phức nghịch đảo cơ bản mà bạn cần phải nắm rõ:
Bài 1 (trong bài 6 trang 144 của sách giải tích 12)
Trong các kết luận dưới đây, kết luận nào sai?
A: Modun số phức z là một số thực không âm
B: Modun số phức z là một số phức
C: Modun số phức z là một số thực dương
D: Modun số phức z là một số thực
Hướng dẫn giải:
Do Số phức z = 0 có môđun |z| = 0. Vì thế modun của số phức z vẫn bằng được 0.
=> Đáp án là C là đáp án đúng
Xem thêm:
Công thức nội suy là gì? Hướng dẫn tính từ A – Z
Đồng quy là gì? Thế nào là 3 đường thẳng đồng quy?
Bài 2 (trong bài 5 trang 144 sách Giải Tích lớp 12)
Biết rằng, nghịch đảo của số phức z bằng với số phức liên hợp của nó. Trong các kết luận ở dưới đây thì kết luận nào là đúng nhất?
A: z R
B: |z| = 1
C: |z| = -1
D: z là một số thuần ảo
Hướng dẫn giải:
Trong số phức z thì ta có
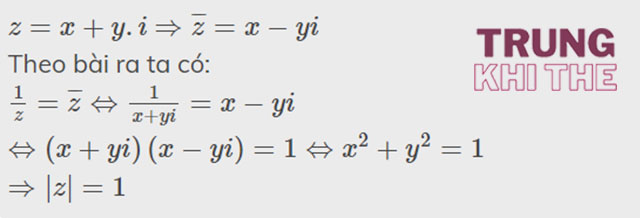
=> Đáp án là B là đáp án đúng
Bài 3 (Phép cộng và nhân các số phức)
Cho hai số phức z = a + bi; z’ = a’ + b’i. Chọn công thức đúng:
- z+z’=z+z’=(a+b)+(a’+b’)ia+b+a’+b’i
- z−z’=z-z’=(a+b)−(a’+b’)ia+b-a’+b’i
- zz’=zz’=(aa’−bb’)+(ab’+a’b)iaa’−bb’+ab’+a’bi
- zz’=zz’=(aa’+bb’)−(ab’+a’b)i
Hướng dẫn giải:
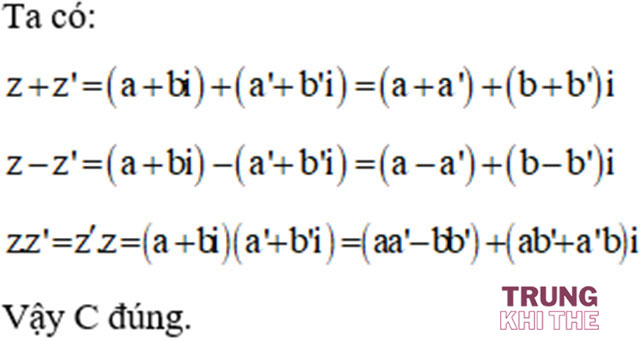
=> Đáp án là C là đáp án đúng
Bài 4 (Phép chia số phức)
Số phức z thỏa mãn z(1 + 2i) + 1 – i = 2i là
- -1+i
- 1-i
- 1+i
- -1-i
Hướng dẫn giải:
Ta có: z(1 + 2i) + 1 – i = 2i ⇔ z(1 + 2i) = -1 + 3i
Vì thế ta được

=> Đáp án là C là đáp án đúng
Bài 5 (Phương trình bậc hai với hệ số thực)
Căn bậc hai của số a = −3a = -3 là:
- 3i3i và −3i-3i.
- 3√i3i và −3√i-3i.
- i√3i3 và −i√3-i3.
- √3i3i và −√3i-3i.
Hướng dẫn giải:
Căn bậc hai của số a=−3a=-3 là i√3i3 và −i√3-i3.
=> Đáp án là C là đáp án đúng
Mẹo giải bài tìm số phức nghịch đảo qua máy tính cầm tay Casio
Ngày nay, ta có thể dễ dàng giải các bài tập về số phức nghịch đảo qua máy tính bỏ túi casio FX 570E. Đây là cách giúp các học sinh tiết kiệm thời gian cũng như gia tăng độ chính xác trong quá trình làm bài tập.
Để thực hiện, ta cần làm theo từng bước dưới đây.
Bước 1: Ấn vào phím More 2 để vào được phần phương trình tính toán số phức của máy tính Casio.
Bước 2: Tiếp đến nhập số phức z = a + bi theo mẫu mà đề bài đã cho.
Bước 3: Kết quả sẽ hiện lên sau khi ta ấn nút “=”.

Ví dụ thực hành
Ta có đề bài là tìm số phức nghịch đảo của số phức z = 2 – i3. Theo đó ta sẽ thực hiện theo những bước sau:
Bước 1: Bấm nút Mode 2 để máy tính khởi động chương trình tính toán số phức
Bước 2: Nhập đề bài z = 2 – i3 vào máy tính vào máy tính .
Bước 3: Sau khi nhập xong, ta ấn “=”. Máy tính sẽ hiện kết quả là 25 + 35 i.
Từ đó ta có phố phức nghịch đảo của z = 2 – i3 là bằng 25 + 35 i.
Hy vọng với bài viết này đã giúp bạn hiểu rõ hơn số phức nghịch đảo là gì? Mới đầu có vẻ phức tạp nhưng các bài tập về số phức nghịch đảo hoàn toàn không khó. Chỉ cần bạn chú tâm ôn luyện thì chắc chắn sẽ dễ dàng vượt qua.

 Website đang chạy thử nghiệm
Website đang chạy thử nghiệm