Trong hình học giải tích thì các dạng bài về đồng quy là một trong những dạng bài phổ biến nhất trong cả chương trình toán học cấp 2 lẫn cấp 3. Vậy bạn có thực sự hiểu rõ được đồng quy là gì? Có những cách nào để chứng minh được ba đường thẳng đồng quy không. Cùng Trungkhithe tìm hiểu trong bài viết dưới đây nhé.
Contents
Đồng quy là gì?
Đầu tiên, ta cần tìm hiểu định nghĩa về đồng quy là gì. Theo đó thì Đồng có nghĩa là song hành, cùng nhau sát cánh. Quy là tập trung, hội tụ tại một điểm. Do đó Đồng Quy chính là cùng nhau gặp lại tại một điểm cụ thể.

Ba đường thẳng đồng quy là gì?
Ba đường thẳng đồng quy là nếu cho ba đường thẳng lần lượt là a, b, c không trùng nhau. Nếu cả ba đường thẳng này cùng đi qua một điểm O thì ba đường thẳng này được gọi là ba đường thẳng đồng quy.
Để 3 đường thẳng đồng quy trong tam giác có định lý, tính chất gì?
Định lý tâm bàng tiếp tam giác
Có tia phân giác trong của tam giác cắt với tia phân giác của góc ngoài tại hai đỉnh còn lại tại một điểm. Thì điểm này chính là tâm bàng tiếp của một tam giác. Và một tam giác sẽ có ba tâm bàng tiếp.
Định lý tâm đường tròn ngoại tiếp tam giác
Ba đường trung trực của một tam giác luôn đồng quy tại một điểm và điểm này được gọi là tâm đường tròn ngoại tiếp của một tam giác. Do đó nếu hai đường trung trực của tam giác cắt nhau tại một điểm thì đường trung trực thứ 3 cũng đi qua điểm đó. Và điểm này cách đều ba đỉnh của một tam giác.
Định lý trọng tâm tam giác
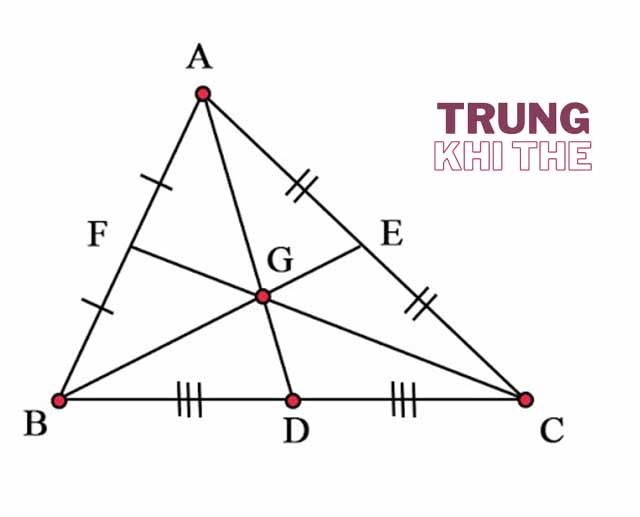
Ba đường trung tuyến của một tam giác dùng đồng quy tại một điểm thì điểm này được gọi là trọng tâm của tam giác. Và khoảng cách từ điểm này đến đỉnh sẽ có khoảng cách gấp đôi so với từ điểm này đến trung điểm của cạnh đối diện. Nếu hai đường trung tuyến trong tam giác cùng cắt tại một điểm thì đường trung tuyến thứ ba cũng đi qua điểm đó.
Định lý tâm nội tiếp tam giác
Ba đường thẳng phân giác của tam giác cùng đồng quy tại một điểm thì điểm này được gọi là tâm nội tiếp của tam giác. Và nếu hai đường phân giác của một tam giác cùng cắt nhau tại một điểm thì đường phân giác thứ ba cũng sẽ đi qua điểm đó. Và tại điểm này sẽ cách đều ba cạnh của tam giác.
Xem thêm:
Số phức nghịch đảo là gì? Toàn tập về số phức nghịch đảo
Công thức nội suy là gì? Hướng dẫn tính từ A – Z
Định lý trực tâm tam giác
Ba đường cao của tam giác đồng quy tại một điểm thì điểm đó được gọi là trực tâm của tam giác.
Hướng dẫn chứng minh 3 đường thẳng đồng quy
Cho ba đường thẳng lần thượt là a, b, c không trùng nhau. Ba đường thẳng a, b, c chỉ được gọi là đồng quy khi ba đường thẳng này cùng đi qua một điểm nào đó. Ta có thể dùng phương pháp ba đường thẳng đồng quy để giải các bài toán trong hình học mặt phẳng, không gian và hàm số đại số.
Trong bài tập hình học mặt phẳng
Ta có thể chứng minh 3 đường thẳng đồng quy theo 7 cách cụ thể sau:
Cách 1: Để chứng minh được ba đường thẳng cùng đồng quy tại một điểm thì ta cần xác định được giao điểm của hai trong ba đường thẳng đó rồi sau đó mới thực hiện chứng minh rằng đường thẳng thứ ba đi qua giao điểm đó.
Cách 2: Chứng minh rằng tại một điểm bất kỳ cũng thuộc vào ba đường thẳng đó.
Cách 3: Áp dụng một trong các chất đồng quy của tam giác là: Ba đường thẳng có chứa các đường trung tuyến, Ba đường thẳng có chứa các đường trung trực, Ba đường thẳng có chứa các đường phân giác, Ba đường thẳng có chứa các đường các đường cao.
Cách 4: Dùng tính chất của đường thẳng để định ra trên hai đường thẳng song song và các đoạn thẳng tỉ lệ.
Cách 5: Dùng cách phản chứng bằng cách giả sử đường thẳng đã cho không đồng quy và từ đó dẫn tới hệ quả vô lý để chứng minh được ba đường thẳng đồng quy..
Cách 6: Dùng tính chất thẳng hàng của các điểm
Cách 7: Chứng minh rằng các đường thẳng này đều đi qua một điểm duy nhất.
Trong bài tập hình học không gian
Ví dụ: Cho 3 đường thẳng a, b, c trong không gian. Chứng minh ba đường thẳng này đồng quy tại một điểm cố định
Đáp án:
Cách 1: Áp dụng nguyên lý cơ bản
Tìm I=a∩b
Tìm hai mặt phẳng (P),(Q) chứa ( I ) sao cho thỏa mãn c = (P) ∩ (Q). Khi đó hiển nhiên I ∊ c
Cách 2: Sử dụng định lý, nếu 3 mặt phẳng có chứa 3 đường thẳng a, b, c đôi một cắt nhau theo 3 giao tuyến. Thì khi đó 3 giao tuyến đó sẽ song song hoặc đồng quy với nhau. Tiếp đến ta cần chứng minh 3 đường thẳng a, b, c không cùng nằm trên một mặt phẳng phẳng và cắt nhau đôi một.
Đồng quy rất quan trọng trong hình học không gian
Trong bài tập đồ thị hàm số
Trong dạng bài tập hàm số trong phần đại số thì để chứng minh được ba đường thẳng đồng quy tại một điểm thì ta dùng phương pháp tìm giao điểm của hai đường thẳng và chứng minh đường thẳng còn lại đi qua giao điểm đó.
Ví dụ: Cho mặt phẳng (Oxy), có 3 phương trình đường thẳng là:
(a) x-y+6=0, (b) 3x-y+7=0, (c) (m-2)x+y-1=0
Tìm m để 3 đường thẳng a, b, c đồng quy tại 1 điểm.
Đáp án:
Gọi (O) là giao điểm của 2 đường thẳng a và b. Khi đó O sẽ có tọa độ là nghiệm của hệ phương trình: x-y+6=0 và 3x-y+7=0 → O ( -12 ,112)
Và để 3 đường thẳng đồng quy thì O( -12 ,112) ∊ (c) → (m-2).(-12)+112-1=0⇔m=11
Hy vọng qua bài viết này đã giúp bạn nắm vững được những kiến thức cơ bản về đồng quy là gì? Đồng quy là kiến thức cơ bản trong toán học và góp mặt trong rất nhiều bài tập quan trọng. Chúc bạn áp dụng thành thục đồng quy vào trong các bài toán.

 Website đang chạy thử nghiệm
Website đang chạy thử nghiệm